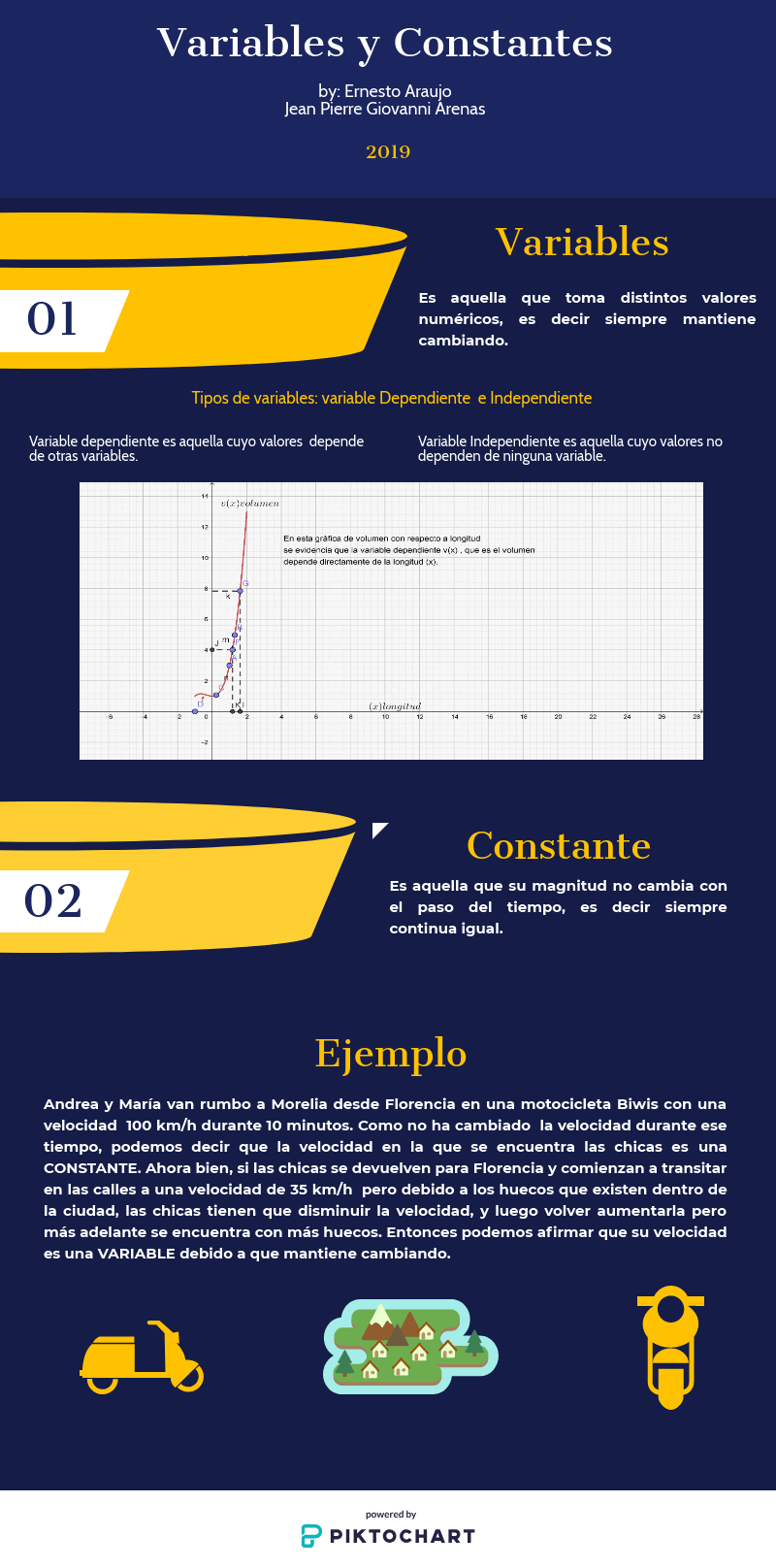
Derivada como razón de cambio
Introducción
En esta OVA (objeto virtual de aprendizaje), se desarrollará una temática asociada al concepto de derivada desde la
razón de cambio, ésta contiene los objetivos de aprendizaje asociados al contenido temático. Además, del contenido
desarrollado como lo es las variables, constantes, función, pendientes, rectas secantes y rectas tangentes. Así
mismo,
videos infografías que ayudan a retroalimentar y apropiarse del concepto de derivada como razón de cambio. Por
ultimo
dentro de la misma se tiene una evaluación con retroalimentación que ayudar al fortalecimiento del concepto de la
derivada.
La importancia de esta OVA, es que busca el fortalecimiento de la derivada como razón de cambio, estableciendo unas
características fundamentales para que el estudiante interactúe y establezca relaciones entre el contenido y el
contexto
principalmente. Y con eso poder obtener un aprendizaje más significativo del contenido matemático la derivada.
En cuanto a lo metodológico es importante resaltar la estructura que se implementó en el diseño de los recursos y
materiales de tal manera que impacten en el aprendizaje de los estudiantes. Además, la estructura del OVA se diseño
a
partir del diseño instruccional ASSURE donde dicha estructura es secuencial estableciendo así mismo un aprendizaje
secuencial.
Objetivos
General
Fortalecer el aprendizaje sobre la derivada como razón de cambio por medio recursos educativos digitales.
Especificos
- Contextualizar conceptos relacionados con la derivada (variables, constantes, funciones, optimización, rectas secantes, rectas tangentes, entre otros).
- Resolver situaciones problemas de la cotidianidad de los estudiantes relacionadas directamente con la derivada como razón de cambio.
- Ejercitar los conceptos de la derivada como razón de cambio.

Conceptualización
Ejemplos practicos
Ejemplo 1
Se desea construir cajas de cartón sin tapa partiendo de cuadrados de lado 40 cm al que se les recortan las esquinas como indica la figura, luego se dobla a lo largo de las líneas punteadas.
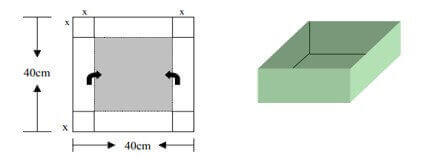
a. ¿Es necesario que el recorte en las esquinas sea cuadrado?
b. Determina la longitud x de los recortes para el volumen de la caja sea Máximo, así como también el valor de ese volumen máximo.
Una vez armada, la caja tendrá como base un cuadrado de lado . Su volumen estará dado por la expresión
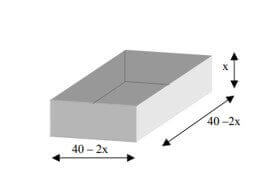
Estudiaremos la función en el intervalo
Valores en los extremos:
Busquemos puntos críticos.
Derivando:
Anulando obtenemos como puntos críticos:
y
Para clasificar el punto crítico interior al intervalo estudiemos el signo de la derivada primera.
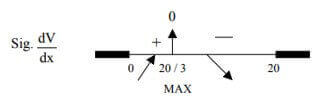
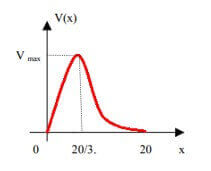
El valor corresponde pues a un máximo. El
bosquejo grafico de la función V es el que indica la figura.corresponde pues a un máximo. El bosquejo gráfico de la función $\mathbb{V}$ es el
que indica la figura.
Observa que la curva tiene tangente horizontal en ya que en ese valor la derivada es nula.
El correspondiente volumen será:
Ejemplo 2
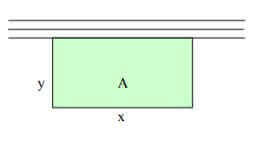
Como el costo del alambre es proporcional a la longitud y los cinco tiros son iguales, bastara minimizar el costo de uno de ellos.
Llamemos L a su longitud expresada en (m) y A el área encerrada en . Tendremos: L= x+2y y deberá cumplirse la condición x.y=A (1) despejando a (y) de (1) y sustituyendo obtenemos la función L.
Derivando para hallar putos críticos:
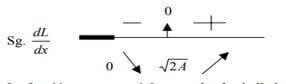
La función presenta mínimo en el valor hallado de x. el correspondiente valor de Y deducido de la expresión (1) será:
El ancho del rectángulo a alambrar es entonces la mitad del largo. Siendo 1 Hec.=10.000
Como el alambre tiene 5 hilos, la longitud total de alambre será:
El costo total del alambre asciende a la suma de $ 156,52.
Si deseas tener un costo más ajustado del trabajo de almacenamiento deberás agregar el contó de los postes, el de os piques, el salario del alumbrador y estimar además un porcentaje de alambre para ataduras y de desperdicio.
Ejemplo práctico

Evaluación
Bibliografia
- Autoridad, N. D. E., La, P., & Documentos, R. Y. A. D. E. (2011). Este documento impreso se considera copia no controlada. 1.
- Impreso se considera copia no controlada. 1. Benítez Lima ; María Gregoria. (n.d.). EL MODELO DE DISEÑO INSTRUCCIONAL ASSURE APLICADO A LA EDUCACIÓN A DISTANCIA. Retrieved June 24, 2019, from https://www.researchgate.net/publication/46562749_EL_MODELO_DE_DISENO_INSTRUCCIONAL_ASSURE_APLICADO_A_LA_EDUCACION_A_DISTANCIA
- Centro de Investigación en Matemáticas A.C. (n.d.). VALORES MÁXIMOS Y MÍNIMOS. Retrieved from https://www.cimat.mx/ciencia_para_jovenes/bachillerato/calculo_diferencial_2015/stewart_cap4.pdf
- Colo, A., Patritti, H., Ana, P., Herrera, C., & Patritti, P. H. (n.d.). APLICACIONES DE LA DERIVADA APLICACIONES DE LA DERIVADA Ejercicios resueltos. Retrieved from http://www.x.edu.uy/liceo26/patritti.pdf
- (Ejercicios para aprender a derivar Derivación de polinomios y series de potencias, n.d.)Ejercicios para aprender a derivar Derivación de polinomios y series de potencias. (n.d.). Retrieved from www.academialasrozas.com
Créditos
Autores
Ernesto Araujo Chavarro
Jean Pierre Giovanni Arenas Ortiz
Especialización TIC para la Innnovación en la Educación
